20 mars 2024
La théorie des nœuds JMV16062015,
C’est que la théorie des nœuds explique, montre, c’est un exemple parfait pour montrer que la question de Leibniz qui était de savoir : si la connaissance de la structure interne d’un objet permettait de prévoir toutes les situations où il peut se trouver ?, quand il se trouve dans un espace donné !, et bien la réponse est ... non !
Puisque les nœuds, on connait parfaitement la structure du tore, et la structure du rond de ficelle, c’est pas la connaissance de ce cercle déformé, trigonométrique, continument, que je peux même dessiner comme ça,
qu’on peut appeler un cycle, c’est un trajet fermé, V01- 28.08 ;
La connaissance du cycle ne donne pas la théorie des nœuds, on est bien embêté, parce qu’on ne sait pas comment les classifier, ça c’est ce dont on va parler la semaine prochaine !
C’est la différence entre les nœuds logiques et les nœuds topologiques,
Les nœuds logiques que j’écris comme des plongements à la place du cercle, je prends cette logique et je l’écris (u , V) vous avez ici quelque chose qui est très facilement classifiable, parce que les deux lettres que vous allez choisir pour chaque nœud logique, vous pouvez les distinguer, et vous pouvez selon l’espace où vous choisissez de construire ces nœuds logiques, vous allez pouvoir avoir une classification automatique,
Donc dans la topologie des nœuds, la structure extrinsèque des nœuds est beaucoup plus compliqué que la structure extrinsèque des nœuds logiques,
Dans la logique c’est plutôt la structure extrinsèque qui est compliquée, c’est toute cette structure linéaire de l’algèbre (en bas gauche du tableau) que j’ai commencé à exposer où il y a le calcul des propositions,
voyez vous avez ça (S2T2) et que ceci (S2T2) ça va être un métalangage de ça (S1T1),
vous avez ceci (S1T1), ça c’est le calcul des prédicats quantifiés, V02-24.28,
Ici ( S2T2) vous avez les connecteurs comme la négation, (¬ ), le Ou, (∨), le Et, (∧), l’implication,(⇒),
et là (S1T1) vous avez la quantification, avec Pourtout, (∀), et Il existe, (∃).
Mais ça (S1T1), c’est le calcul de la coordination et des concepts.
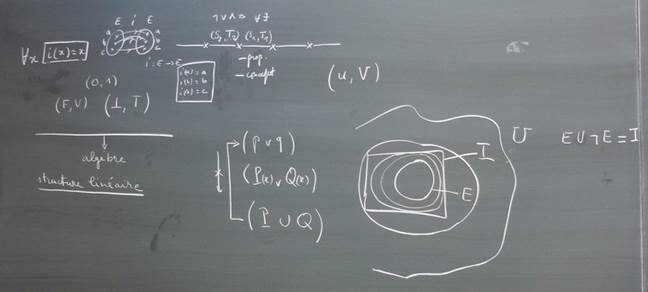
cliquer sur la photo pour l'agrandir,
Parce qu’ici, en S1T1, vous avez des propositions, et des concepts,
Alors ici en S2T2 et en S1T1 !?
Pourquoi appeler ça Calcul des propositions ?
C’est le calcul des propositions et des concepts, c’est ce que j’expliquais la semaine dernière !
Donc appelons ça (S2T2), autrement, on va appeler ça (S2T2) : Calcul de la coordination, c’est la coordination aussi bien des propositions que des concepts,
Quand vous écrivez p ∨ q, c’est une coordination de deux propositions, V02-25.16,
Si p et q sont des propositions, mais si vous écrivez ça comme ça ( P(x) ∨ Q(x) ), c’est même ce qui va faire confondre la disjonction logique (p∨q) avec le ∨ des concepts ( P(x) ∨ Q(x) ), qui ressemble à l’union des ensembles, ∪ , l’ensemble ( P ∪ Q )
et je vous dis que :
c’est toujours une erreur d’expliquer la Logique par la Théorie des ensembles parce que c’est le contraire,
c’est la Théorie des ensembles qui peut être écrite grâce à la Logique.
( ici c’est ( P(x)∨ Q(x) ), qui peut être écrit grâce à la logique (p∨q) ). )
Mais c’est pas réciproque, ça ne marche pas dans l’autre sens,
( La Logique ne peut pas être écrite, décrite à partir de la Théorie des ensembles ) et vous avez une perte si vous oubliez de faire de la Logique, si vous croyez par exemple que la négation c’est le complémentaire ensembliste.
En Logique la négation n’est pas le complémentaire ensembliste, à la rigueur ce serait la négation d’une proposition ou d’un concept.
Si c’était un ensemble, qu’est ce que c’est que la négation ?
C’est le plus petit ensemble de la famille des sous-ensembles, qu’il faut ajouter à un ensemble pour obtenir l’ensemble complet, je vous montre ça sur un dessin,
V02 renvoie à la vidéo numéro 2, et 24.28 à la position temporelle du texte dans la vidéo.
1.28.08 renvoie à la position temporelle du texte dans le MP3 de ce cours !
disponibles sur TEE topologie
ST, Système_Syntaxe/ Théorie,
Adieu !, l’initiation c’est fini … ! .et D’une autre façon d’être Ensemble !!
Il n’a pas tort, mais à mon avis Boole ça permet de faire beaucoup mieux, par exemple de ne plus pratiquer l’initiation, puisque la mathématique grâce à Cantor, on arrive à un degré d’écriture et de pratique de l’écriture qui est enseignable, et qui ne nécessite plus du tout de pratique des initiations, avec des gestes obscènes, et des choses qui concernent les orifices du corps, parce que l’initiation c’est faire enter les idéaux de la société, du groupe, dans le corps, par les orifices,
Lacan nous dit qu’avec Cantor c’est terminé ça, pourquoi ?, parce que même les mathématiques c’est enseignable, grâce à Cantor, et grâce à la théorie des ensembles,
Avec Lacan on peut corriger l’objet, dans une lettre qui n’est pas parue dans les Autres écrits, qui a glissée sous la table, parce que dans cette lettre il ajoute :
" et c’est pour ça que j’ai réduit la psychanalyse à la théorie des ensembles",
Ce qui peut paraître un peu fort de roquefort, c’est exagéré de dire qu’il a réduit la psychanalyse à la théorie des ensembles !
Mais qu’est ce qu’il a fait Lacan ? : Il a réduit les formules de la sexuation, sont écrites en théorie des ensembles, avec ce système d’écriture là, des propositions et des concepts, avec les quanteurs.
Et les quanteurs il va en inventer deux nouveaux, ça c’est une autre affaire, mais j’ai écrit là-dessus, ça se trouve dans la page internet, qui est accessible sur internet.